Volume Rendering and Neural Radiance Fields

Overview

This project explores advanced techniques in neural volume and surface rendering for creating realistic 3D scenes from 2D images. The goal is to leverage deep learning methods to learn 3D representations and render high-quality images from novel viewpoints.

Technical Details

Differentiable Volume Rendering

We implement a differentiable volume renderer using PyTorch, which allows for end-to-end optimization of scene parameters using image supervision. The renderer is based on the emission-absorption model and uses numerical integration along viewing rays to compute pixel colors.

The renderer is implemented in the renderer.py file and uses the VolumeRenderer class. The rendering process involves sampling points along each ray, querying the volume density and color at each point, and compositing the colors using the alpha-blending formula.

Optimizing a Basic Implicit Volume

We define a simple 3D shape (a box) using an implicit representation, where the shape is defined by a signed distance function (SDF). The SDF is implemented as a PyTorch module in the implicit_volume.py file, using the BoxSDF class.

We optimize the parameters of the box (center and size) to match a set of ground truth images using the differentiable renderer. The optimization is performed using the Adam optimizer and the L2 loss between the rendered and ground truth images.

Optimizing a basic implicit volume

Neural Radiance Fields (NeRF)

We implement Neural Radiance Fields (NeRF) using a fully-connected neural network that takes a 3D position and viewing direction as input and outputs the volume density and color at that point. The network architecture and training procedure follow the original NeRF paper[2].

The NeRF model is defined in the nerf.py file, using the NeRF class. The model is trained on a dataset of images with known camera poses, using the differentiable renderer to optimize the network weights. The loss function includes an L2 term for RGB values and a regularization term to encourage smooth density fields[2].

Testing a view dependence NeRF pipeline

Sphere Tracing

We implement sphere tracing, a technique for rendering 3D shapes defined by signed distance functions (SDFs). Sphere tracing iteratively steps along the viewing ray, using the SDF to determine the distance to the nearest surface point[3].

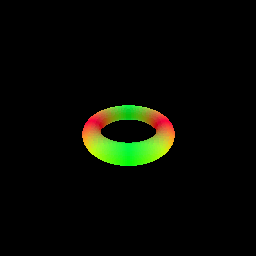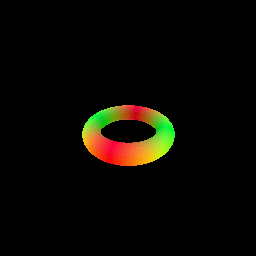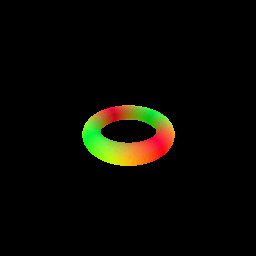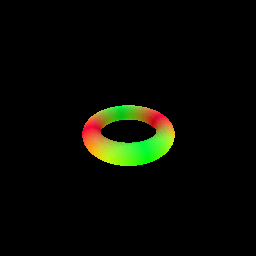
The sphere tracing algorithm is implemented in the sphere_tracing.py file, using the render_sdf function. The function takes an SDF model and camera parameters as input and returns the rendered image. We demonstrate sphere tracing by rendering a torus SDF[3].

Sphere Tracing

Optimizing a Neural SDF

We train a neural network to represent a 3D shape as an SDF, which can be rendered using sphere tracing. The network takes a 3D point as input and outputs the signed distance to the surface at that point[3].

The neural SDF model is defined in the neural_sdf.py file, using the NeuralSDF class. The model is trained on a point cloud of the object, using the L1 loss between the predicted and ground truth signed distances. We use the Eikonal regularization term to encourage the learned SDF to be a valid signed distance function[3].

Neural SDF

VolSDF

We implement VolSDF, a method for learning 3D representations from images by combining neural SDFs and volume rendering. VolSDF converts the SDF into a volumetric representation using a Gaussian density function and renders the volume using the differentiable renderer[4].

The VolSDF model is defined in the volsdf.py file, using the VolSDF class. The model consists of a neural SDF and a Gaussian density function that converts signed distances to volume densities. The model is trained on a dataset of images with known camera poses, using the differentiable renderer and the L2 loss on RGB values[4].

Geometry of Volume SDF

Results

We demonstrate the effectiveness of the implemented techniques on various 3D objects and scenes:

• Optimizing a box shape to match ground truth images using the differentiable renderer.
• Training a NeRF model on a dataset of images and rendering novel views of the scene.
• Rendering a torus SDF using sphere tracing.
• Learning a neural SDF representation of a 3D object from a point cloud.
• Training a VolSDF model on a dataset of images and rendering novel views of the object.

Conclusion

This project showcases the power of neural rendering techniques for learning and visualizing 3D shapes and scenes from 2D images. By leveraging deep learning and efficient rendering algorithms, we can create highly realistic and detailed 3D representations from limited observations.

The implemented techniques, such as differentiable volume rendering, neural radiance fields, sphere tracing, and VolSDF, demonstrate the state-of-the-art in neural rendering and provide a foundation for further research and applications in computer graphics and vision.

References

1. Max Niemeyer, Lars Mescheder, Michael Oechsle, and Andreas Geiger. "Differentiable volumetric rendering: Learning implicit 3d representations without 3d supervision." In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 3504-3515. 2020.
2. Ben Mildenhall, Pratul P. Srinivasan, Matthew Tancik, Jonathan T. Barron, Ravi Ramamoorthi, and Ren Ng. "NeRF: Representing scenes as neural radiance fields for view synthesis." In European Conference on Computer Vision, pp. 405-421. Springer, Cham, 2020.
3. Matan Atzmon and Yaron Lipman. "SAL: Sign agnostic learning of shapes from raw data." In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 2565-2574. 2020.
4. Michael Oechsle, Lars Mescheder, Michael Niemeyer, Thilo Strauss, and Andreas Geiger. "Learning implicit surface light fields." In 2020 International Conference on 3D Vision (3DV), pp. 452-462. IEEE, 2020.